bandsfdp
This package provides functions that compute upper prediction bounds
on the FDP in competition-based setups (see Ebadi et al. (2022)). Such
setups include target-decoy competition (TDC) in computational mass
spectrometry and the knockoff construction in regression. Note we
typically use the terminology of TDC throughout.
In (single-decoy) TDC, each hypothesis is associated to a winning
score and a label (\(1\) for a target
win and \(-1\) for a decoy win).
Functions in this package assume that the hypotheses are ordered in
decreasing order of winning scores (with ties broken at random).
The functions tdc_sb() and tdc_ub() give an
upper prediction bound on the FDP in TDC’s discovery list. Given TDC’s
rejection threshold, the target/decoy labels, and a desired confidence
level \(1 - \gamma\), these functions
return a real number \([\eta\) such
that the FDP in the list of discoveries is \(\leq \eta\) with probability \(\geq 1 - \gamma\).
The function sim_bound() provides simultaneous bounds on
the FDP. It computes an upper prediction bound on the FDP of target wins
among the top \(k\) hypotheses of TDC
(the hypotheses of the \(k\) largest
winning scores), for each \(k =
1,\ldots,n\) where \(n\) is the
total number of hypotheses. Similarly, the function
gen_bound() provides a bound on the FDP among target wins
in an arbitrary set \(R\) of hypotheses
of TDC.
Note that upper prediction bounds are derived from upper prediction
bands. In particular, the bounds in this package are derived from the
standardized band (SB) and uniform band (UB), hence the name
“bandsfdp”.
Installation
You can install the development version of bandsfdp from GitHub with:
# install.packages("devtools")
devtools::install_github("uni-Arya/bandsfdp")
Usage
The standardized and uniform bands require pre-computed Monte Carlo
statistics. These can be downloaded using
devtools::install_github("uni-Arya/fdpbandsdata")
(approximately 81Mb). The user can also view the code used to generate
these tables at fdpbandsdata.
For tdc_sb() and tdc_ub(), the following
inputs are required:
- A vector of (non-negative integer valued) rejection
thresholds. Typically only one is used: the rejection
threshold of TDC.
- A vector of
labels (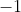 for a decoy win,
for a decoy win, 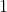 for a target win) that are ordered so the
corresponding winning scores of TDC are decreasing.
for a target win) that are ordered so the
corresponding winning scores of TDC are decreasing.
- A confidence parameter
gamma (a number between 0 and
1), for a 1 - gamma confidence level. Note that the
functions currently support
gamma = 0.01, 0.025, 0.5, 0.1, 0.8, 0.5, but more data can
be generated using the source code at fdpbandsdata.
- The FDR tolerance
alpha used in TDC (a number between 0
and 1).
With a Single Decoy Score
Typically, TDC uses a single decoy score in its competition step.
Hence, both tdc_sb() and tdc_ub() assume this
to be the case by default (the parameters c and
lambda are both set to 0.5 by default).
Below is an example of how to use these functions. Note that the
thresholds are not representative of the actual rejection
threshold of TDC.
suppressPackageStartupMessages(library(bandsfdp))
set.seed(123)
if (requireNamespace("fdpbandsdata", quietly = TRUE)) {
thresholds <- c(250, 500, 750, 1000)
labels <- c(
rep(1, 250),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.9, 0.1)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.5, 0.5)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.1, 0.9))
)
alpha <- 0.05
gamma <- 0.05
print(tdc_sb(thresholds, labels, alpha, gamma))
print(tdc_ub(thresholds, labels, alpha, gamma))
}
#> [1] 0.02000000 0.09453782 0.26825127 0.29575163
#> [1] 0.02400000 0.08823529 0.26315789 0.29084967
With Multiple Decoy Scores
TDC can be extended to use multiple decoys. In that setup, the target
score is competed with multiple decoy scores and the rank of the target
score after competition is used to determine whether the hypothesis is a
target win (label = \(1\)), decoy win
(\(-1\)) or uncounted (\(0\)). The top c proportion of
ranks are considered winning, the bottom 1-lambda losing,
and all the rest uncounted. The parameters c and
lambda must satisfy the following conditions:
- \(c \leq \lambda\)
- \(c\) and \(\lambda\) are of the form \(k/(d+1)\) where \(d\) is the number of decoys used and \(1 \leq k \leq d\) is an integer.
As an example, if we use \(3\) decoy
scores for each hypothesis, we may take \(c\) and \(\lambda\) to be one of \(1/4\), \(1/2\), or \(3/4\), subject to \(c \leq \lambda\). For instance, if \(c = 1/4\), \(H_i\) is labelled as a target win whenever
its corresponding target score is the highest ranked score among all
decoys for that hypothesis.
Below is an illustrative example of such a use.
suppressPackageStartupMessages(library(bandsfdp))
set.seed(123)
if (requireNamespace("fdpbandsdata", quietly = TRUE)) {
thresholds <- c(250, 500, 750, 1000)
labels <- c(
rep(1, 250),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.9, 0.1)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.5, 0.5)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.1, 0.9))
)
alpha <- 0.05
gamma <- 0.05
c <- 0.25
lambda <- 0.25
print(tdc_sb(thresholds, labels, alpha, gamma, c, lambda))
print(tdc_ub(thresholds, labels, alpha, gamma, c, lambda))
}
#> [1] 0.00800000 0.03991597 0.16298812 0.19444444
#> [1] 0.01200000 0.03781513 0.15449915 0.18627451
Interpolated Bands
All bands are interpolated by default, which requires the computation
of a running maximum. This generally results in a slightly tighter
bound, but at the cost of computational power. We recommend the use of
interpolate = TRUE, unless it is too time-consuming.
If one wishes to use non-interpolated bands, the code below shows an
example of such a use.
suppressPackageStartupMessages(library(bandsfdp))
set.seed(123)
if (requireNamespace("fdpbandsdata", quietly = TRUE)) {
thresholds <- c(250, 500, 750, 1000)
labels <- c(
rep(1, 250),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.9, 0.1)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.5, 0.5)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.1, 0.9))
)
alpha <- 0.05
gamma <- 0.05
c <- 0.25
lambda <- 0.25
print(tdc_sb(thresholds, labels, alpha, gamma, c, lambda, interpolate = FALSE))
print(tdc_ub(thresholds, labels, alpha, gamma, c, lambda, interpolate = FALSE))
}
#> [1] 0.00800000 0.03991597 1.00000000 1.00000000
#> [1] 0.01200000 0.03781513 1.00000000 1.00000000
Simultaneous FDP bounds
One may also be interested in computing a bound on the FDP of target
wins among the top \(k\) hypotheses for
all \(k = 1, \ldots, n\), where \(n\) is the total number of hypotheses. In
this case, the function sim_bound() should be used. This
function requires the following arguments:
- A vector of (ordered)
labels, confidence parameter
gamma, and competition parameters c and
lambda, as described in the previous sections.
- A character argument
type which is either
"stband" or "uniband", specifying the type of
band to be used to compute the simultaneous FDP bounds.
- The maximum number of decoy wins considered for the bands
d_max (defaults to NULL, in which case it is
automatically computed using max_fdp below).
- The maximal considered FDP for the simultaneous bounds
max_fdp (defaults to max_fdp = 0.5).
The arguments d_max and max_fdp control the
rate at which the simultaneous bounds are increasing. More information
is written in the details section of the R documentation of
sim_bound(). We also refer the reader to Section 3 of Ebadi et al. (2022) for more
details.
Below is an example of such a use of the function.
suppressPackageStartupMessages(library(bandsfdp))
set.seed(123)
if (requireNamespace("fdpbandsdata", quietly = TRUE)) {
set.seed(123)
labels <- c(
rep(1, 250),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.9, 0.1)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.5, 0.5)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.1, 0.9))
)
gamma <- 0.05
sim_bound(labels, gamma, type = "stband")[700:706]
}
#> [1] 0.2402827 0.2416226 0.2416226 0.2416226 0.2416226 0.2416226 0.2429577
Generalized FDP bounds
One may be interested in computing an upper prediction bound on the
FDP among target wins in an arbitrary set \(R\) of hypotheses. In this case, the
function gen_bound() should be used. Here, one uses the
same arguments as in sim_bound(), with an additional
argument indices that specifies the set of indices \(R\) for which to compute the upper
prediction bound over.
Below is an example of such a use of the function.
suppressPackageStartupMessages(library(bandsfdp))
set.seed(123)
if (requireNamespace("fdpbandsdata", quietly = TRUE)) {
set.seed(123)
labels <- c(
rep(1, 250),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.9, 0.1)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.5, 0.5)),
sample(c(1, -1), size = 250, replace = TRUE, prob = c(0.1, 0.9))
)
indices <- c(1:100, 300:400, 600:650)
gamma <- 0.05
gen_bound(labels, indices, gamma, type = "stband")
}
#> [1] 0.2546296